0.简介
线段树和树状数组是用来解决区间修改和区间查询的数据结构,二者各有优劣,且理解和实现难度不同,因此都需学习。
本文将讲述线段树和树状数组的实现原理和模板题具体实现。
废话不多说,让我们开始吧
1. 线段树
1.1 什么是树
由n-1条边连接n个结点即为树。(草率而不严谨的定义)
树上通常有:儿子,父亲等通俗易懂的名词;入度,出度等需要知道的名词。
二叉树即每个节点都只有左儿子和右儿子两个儿子的树。
二叉树的特性使之应用极广。
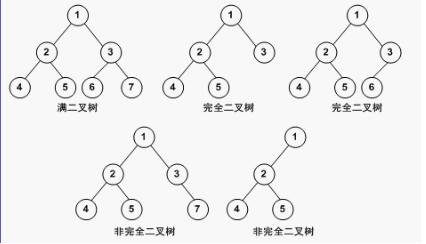
二叉树中,满二叉树和完全二叉树又是值得拎出来说的。
满二叉树即每个结点都有0或2个子结点,导致整棵树的第i层都是2^{i-1}个结点。
完全二叉树即在满二叉树的基础上,最后一行从右向左删去若干个结点构成的。
1.2 二叉树的存储结构
二叉树有很多存储方式,就像数据结构本身就有很多存储方式一样。
我们这里只介绍一种存储结构,也是我们后期线段树用到的存储结构,即层序存储。
一棵二叉树,可以补全为一棵满二叉树。一棵满二叉树按照层序编号,即可将每个结点信息进行存储。
这种存储方式的好处是,我们可以快速的找到一个结点的父亲和两个儿子。比如第i号结点,它的父亲即为a[i/2],它的左儿子为a[i*2],右儿子为a[i*2]+1。
1.3 线段树
讲完先修知识后,我们来看看什么是线段树。
线段树,可以通俗的理解为由线段构成的树或者把线段分成树。
我们先来看一个实例。
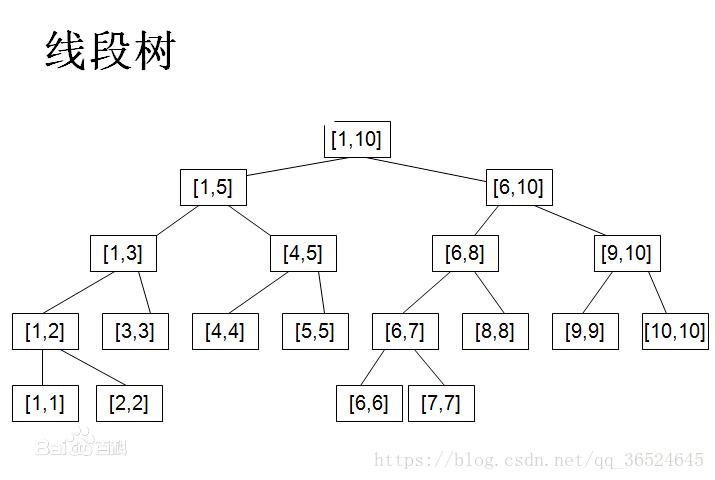
我们可以看到,将线段[1,10]做成线段树,即二分线段作为左右儿子,以此类推。
线段树的用处是,对编号连续的一些点进行修改或者统计操作,复杂度都是O(log2(n))
线段树的原理是,对每个区间的修改可以分解为对若干个子区间的修改,如对[3,8]这个区间进行修改,只需要对[3,3],[4,5],[6,8]这三个点进行修改即可,区间求和同理。具体实现我们慢慢来讲。
由此看出,用线段树统计的东西,必须符合区间加法,否则,不可能通过分成子区间来得到结果。
1.4 线段树的实现原理
线段树有很多操作,如单点修改,区间修改,单点查询,区间查询等,我们挨个说。
线段树一般会维护区间内的一个内容,如区间和,最大值,最小值等等。
以下内容由上图即[1,10]举例。
1.4.1 线段树的单点修改
单点修改是很简单的,简单的像单点查询一样。
假设我们要修改[5,5]的值,我们只需要修改[5,5],[4,5],[1,5],[1,10]即可。时间复杂度为O(log2(n))
1.4.2 线段树的单点查询
单点查询是很简单的,简单的像单点修改一样。
假设我们要查询[5,5]的值,我们可以直接访问该结点即可。至于结点序号,有了n就能推出来了。就算推不出来,还可以通过[1,10]→[1,5]→[4,5]→[5,5]来逐步找到该结点。时间复杂度为O(log2(n))
1.4.3 线段树的区间查询
区间查询,即可将要查询的区间分成若干个区间,然后将这些区间的信息合并即为要查询的信息。就如上文所提到的,如果我们要查询[3,8]这个区间,就可以将[3,3],[4,5],[6,8]三个区间的信息合并得到。
这里引入一个定理:当n≥3时,一个[1,n]的线段树可以将[1,n]的任意子区间[L,R]分解为不超过2\lfloor log_2 (n-1)\rfloor个子区间。因此区间查询的时间复杂度为O(log2(n))。定理证明
1.4.4 线段树的区间修改
与区间查询类似,区间修改也是将区间分成若干子区间操作的。
与区间查询不同的是,在区间修改时我们引入了lazy标记,即懒惰标记,也叫延迟标记。
标记的用处是:标明本节点的信息已经根据标记更新过了,但子结点及子树仍需要更新
举个例子,假设我们要给[3,8]这个区间内每个值都加1,那么实际上,只改变[3,3],[4,5],[6,8]这三个结点,而它们的子树还没有变。我们在这三个结点处打上lazy标记,对于[6,8]这个结点,我们要加3(即678)。这样向下的修改就被我们延迟下来了。但是向上显示的信息却是修改后的结果,比如我们要查询[6,10],是由[6,8],[8,10]两个区间组成,其中[6,8]的值已经变了,因此保证我们查询的是正确结果。当我们需要查询子树的信息时,再将lazy标记下推即可。
标记有相对标记和绝对标记之分:
绝对标记如将区间所有数+x,标记间可以共存,和打标记的顺序无关。因此我们可以区间修改时不下推标记,等到查询时再下推。
绝对标记如将区间内所有数变成x,打标记的顺序会直接影响结果,所以这种标记在区间修改时必须下推旧标记,否则会出错。
值得注意的是,有多个标记时,标记下推的顺序也很重要,错误的下推顺序可能会导致错误。
1.5 线段树的递归实现
例6:[模板]线段树2:luoguP3373:传送门
题目大意:一个数列,区间修改,区间查询。其中区间修改有区间乘和区间加两种。
解题思路:我们构造一棵线段树,维护每个区间的sum值,然后设两个lazy标记,一个叫add代表加法lazy标记,一个叫mu代表乘法lazy标记。
先放个整体代码,然后我们分块去讲每个函数的含义。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <cstdio> using namespace std; int n, m, MOD; int a[100010]; struct node { long long l, r, sum, mu, add; }t[400010]; void build(int x, int l, int r) { t[x].mu = 1; t[x].l = l; t[x].r = r; if (l == r) { t[x].sum = a[l] % MOD; return; } int mid = (l + r) / 2; build(x * 2, l, mid); build(x * 2 + 1, mid + 1, r); t[x].sum = (t[x * 2].sum + t[x * 2 + 1].sum) % MOD; } void spread(int x) { //cout << x << " " << t[x].l << " " << t[x].r << " " << t[x].add << " " << t[x].mu << " " << t[x].sum << endl; t[x * 2].sum = (t[x * 2].sum * t[x].mu + (t[x * 2].r - t[x * 2].l + 1) * t[x].add % MOD) % MOD; t[x * 2 + 1].sum = (t[x * 2 + 1].sum * t[x].mu + (t[x * 2 + 1].r - t[x * 2 + 1].l + 1) * t[x].add % MOD) % MOD; t[x * 2].mu = (t[x * 2].mu * t[x].mu) % MOD; t[x * 2 + 1].mu = (t[x * 2 + 1].mu * t[x].mu) % MOD; t[x * 2].add = (t[x * 2].add * t[x].mu % MOD + t[x].add) % MOD; t[x * 2 + 1].add = (t[x * 2 + 1].add * t[x].mu % MOD + t[x].add) % MOD; t[x].mu = 1; t[x].add = 0; } void mu(int x, int l, int r, int k) { if (t[x].l >= l && t[x].r <= r) { t[x].add = (t[x].add * k) % MOD; t[x].mu = (t[x].mu * k) % MOD; t[x].sum = (t[x].sum * k) % MOD; return; } spread(x); int mid = (t[x].l + t[x].r) / 2; if (l <= mid)mu(x * 2, l, r, k); if (mid < r)mu(x * 2 + 1, l, r, k); t[x].sum = (t[x * 2].sum + t[x * 2 + 1].sum) % MOD; } void add(int x, int l, int r, int k) { if (t[x].l >= l && t[x].r <= r) { t[x].add = (t[x].add + k) % MOD; t[x].sum = (t[x].sum + k * (t[x].r - t[x].l + 1) % MOD) % MOD; return; } spread(x); int mid = (t[x].l + t[x].r) / 2; if (l <= mid)add(x * 2, l, r, k); if (mid < r)add(x * 2 + 1, l, r, k); t[x].sum = (t[x * 2].sum + t[x * 2 + 1].sum) % MOD; } long long ask(int x, int l, int r) { if (t[x].l >= l && t[x].r <= r)return t[x].sum; spread(x); int summ = 0; int mid = (t[x].l + t[x].r) / 2; if (l <= mid)summ = (summ + ask(x * 2, l, r)) % MOD; if (mid < r)summ = (summ + ask(x * 2 + 1, l, r)) % MOD; return summ; } int main() { scanf("%d%d%d", &n, &m, &MOD); for (int i = 1; i <= n; i++)scanf("%d", &a[i]); build(1, 1, n); while (m--) { int c, x, y, k; scanf("%d%d%d", &c, &x, &y); if (c == 1) { scanf("%d", &k); mu(1, x, y, k); } if (c == 2) { scanf("%d", &k); add(1, x, y, k); } if (c == 3) { printf("%lld\n", ask(1, x, y)); } } return 0; } |
1.5.0 定义
|
1 2 3 4 5 |
struct node { long long l, r, sum, mu, add; }t[400010]; |
这里我们定义一个结构体表示这棵树。
其中t[i]表示第i号结点。具体结点编号请参考上面二叉树的存储结构。
每个结点内包含五个量,其中,l表示该结点所表示区间的左端点,r表示该结点所表示区间的右端点,sum表示该结点表示区间的和,mu表示该结点的乘法lazy标记,add表示该结点的加法lazy标记。
1.5.1 建树(初始化)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
void build(int x, int l, int r) { t[x].mu = 1; t[x].l = l; t[x].r = r; if (l == r) { t[x].sum = a[l] % MOD; return; } int mid = (l + r) / 2; build(x * 2, l, mid); build(x * 2 + 1, mid + 1, r); t[x].sum = (t[x * 2].sum + t[x * 2 + 1].sum) % MOD; } |
这个函数就是用来建树的。
函数有三个形参,其中x代表第x号结点,l表示结点的左编号,r表示结点的右编号。
然后我们把x结点的左右区间赋成l和r,将mu标记初始化为1(很好理解,就像你要求几个数的乘积,初始的sum一定等于1)。
然后,如果l==r,说明我们已经推到一个点了,那么这个点的sum值就等于a数组对应的值。
如果l!=r,我们就递推下面的区间(用二分),最后这个点的sum值等于它左右儿子sum值的和。
1.5.2 下传标记(spread函数)
|
1 2 3 4 5 6 7 8 9 10 11 |
void spread(int x) { t[x * 2].sum = (t[x * 2].sum * t[x].mu + (t[x * 2].r - t[x * 2].l + 1) * t[x].add % MOD) % MOD; t[x * 2 + 1].sum = (t[x * 2 + 1].sum * t[x].mu + (t[x * 2 + 1].r - t[x * 2 + 1].l + 1) * t[x].add % MOD) % MOD; t[x * 2].mu = (t[x * 2].mu * t[x].mu) % MOD; t[x * 2 + 1].mu = (t[x * 2 + 1].mu * t[x].mu) % MOD; t[x * 2].add = (t[x * 2].add * t[x].mu % MOD + t[x].add) % MOD; t[x * 2 + 1].add = (t[x * 2 + 1].add * t[x].mu % MOD + t[x].add) % MOD; t[x].mu = 1; t[x].add = 0; } |
下传标记是线段树区间修改中最重要的操作。
下传标记时,本结点的mu和add标记会影响儿子结点的sum值、mu和add标记。
具体的下传参考代码。
下传完毕后,要记得将本结点的标记清空。
1.5.3 区间修改
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
void mu(int x, int l, int r, int k) { if (t[x].l >= l && t[x].r <= r) { t[x].add = (t[x].add * k) % MOD; t[x].mu = (t[x].mu * k) % MOD; t[x].sum = (t[x].sum * k) % MOD; return; } spread(x); int mid = (t[x].l + t[x].r) / 2; if (l <= mid)mu(x * 2, l, r, k); if (mid < r)mu(x * 2 + 1, l, r, k); t[x].sum = (t[x * 2].sum + t[x * 2 + 1].sum) % MOD; } void add(int x, int l, int r, int k) { if (t[x].l >= l && t[x].r <= r) { t[x].add = (t[x].add + k) % MOD; t[x].sum = (t[x].sum + k * (t[x].r - t[x].l + 1) % MOD) % MOD; return; } spread(x); int mid = (t[x].l + t[x].r) / 2; if (l <= mid)add(x * 2, l, r, k); if (mid < r)add(x * 2 + 1, l, r, k); t[x].sum = (t[x * 2].sum + t[x * 2 + 1].sum) % MOD; } |
本题区间修改涉及两种操作,分别是区间乘和区间加。
两者在递推的时候,操作都是一样的:先推标记,再逐步向下递推,最后修改本结点的sum值。
(t[x].l >= l && t[x].r <= r)判断的是该结点的区间是否在大区间内,如果是,则:
区间加很简单,修改本结点的add标记和sum值。
区间乘也很简单,修改本结点的mu标记、add标记和sum值即可。
1.5.4 区间查询
|
1 2 3 4 5 6 7 8 9 10 11 |
long long ask(int x, int l, int r) { if (t[x].l >= l && t[x].r <= r)return t[x].sum; spread(x); int summ = 0; int mid = (t[x].l + t[x].r) / 2; if (l <= mid)summ = (summ + ask(x * 2, l, r)) % MOD; if (mid < r)summ = (summ + ask(x * 2 + 1, l, r)) % MOD; return summ; } |
区间查询直接查找大区间分成的若干个子区间的sum值,加和即可。
在区间加和区间乘混合时,我们一定要注意乘法的优先级,然后在算法中体现。
下面给一个只有区间加的代码,题目是[模板]线段树1:luoguP3372:传送门,大家结合代码自行理解。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
#include <iostream> using namespace std; long long a[100010]; long long n, m; struct node { long long l, r, sum, add; }t[1000010]; void build(long long x, long long l, long long r) { t[x].l = l; t[x].r = r; if (l == r) { t[x].sum = a[l]; return; } long long mid = (l + r) / 2; build(x * 2, l, mid); build(x * 2 + 1, mid + 1, r); t[x].sum = t[x * 2].sum + t[x * 2 + 1].sum; } void push(long long x) { t[x * 2].sum += (t[x * 2].r - t[x * 2].l + 1) * t[x].add; t[x * 2 + 1].sum += (t[x * 2 + 1].r - t[x * 2 + 1].l + 1) * t[x].add; t[x * 2].add += t[x].add; t[x * 2 + 1].add += t[x].add; t[x].add = 0; return; } void add(long long x, long long l, long long r, long long k) { if (t[x].l >= l && t[x].r <= r) { t[x].add += k; t[x].sum += (t[x].r - t[x].l + 1) * k; return; } push(x); long long mid = (t[x].l + t[x].r) / 2; if (l <= mid)add(x * 2, l, r, k); if (mid < r)add(x * 2 + 1, l, r, k); t[x].sum = t[x * 2].sum + t[x * 2 + 1].sum; } long long ask(long long x, long long l, long long r) { if (t[x].l >= l && t[x].r <= r)return t[x].sum; push(x); long long mid = (t[x].l + t[x].r) / 2, ans = 0; if (l <= mid)ans += ask(x * 2, l, r); if (mid < r)ans += ask(x * 2 + 1, l, r); return ans; } int main() { cin >> n >> m; for (long long i = 1; i <= n; i++)cin >> a[i]; build(1, 1, n); while (m--) { long long c, x, y, k; cin >> c >> x >> y; if (c == 1) { cin >> k; add(1, x, y, k); } if (c == 2) { cout << ask(1, x, y) << endl; } } return 0; } |
2.树状数组
2.1 树状数组简介
树状数组,就是用数组模拟树。
树状数组也用来解决区间上更新和求和的问题。
我们已经学习过线段树了,上述问题线段树也能解决,那么为什么还要学习树状数组呢?
原因有二:一,树状数组的常数小,时间复杂度上如果线段树被卡常就可以考虑树状数组(一般碰不到有人卡线段树的常但是以防脑残出题人)。二,树状数组比线段树稍微好写一些(划重点,好写不等于好理解)。
举个不恰当的例子,我们都知道用字符串可以模拟大数运算,但是没有人会在1+1这种问题上进行字符串模拟(很不恰当,大概理解就好)。
2.2 树状数组是什么
我们先来看一个树状数组:

我们学过用二叉树的方式解决区间问题,即线段树。
那么树状数组可以看成是在二叉树中删除若干个结点组成。
换句话说一个树状数组可以恢复出一棵二叉树。
在这个树状数组中:
c[1]=a[1];
c[2]=a[1]+a[2];
c[3]=a[3];
c[4]=a[1]+a[2]+a[3]+a[4];
c[5]=a[5];
c[6]=a[5]+a[6];
c[7]=a[7];
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8];
……
由此我们可以发现,c[i]=a[i-2^k+1]+a[i-2^k+2]+……a[i],其中k是i的二进制中最低位到最高位连续零的个数,也是i的二进制中最低位1的位权。
举个例子,十进制下的4即二进制下的100,所以c[4]=a[4-2^2+1]+a[4-2^2+2]+a[4-2^2+3]+a[4]
这样存储我们该怎么求和呢?
举个例子,假设我们要求前7个数的和,那么sum_7=c[7]+c[6]+c[4]
所以我们又发现,sum_i=c[i]+c[i-2^{k1}]+c[(i-2^{k1})-2^{k2}]+···,其中2^{k1}为i的二进制中最低位1的位权,2^{k2}为i的二进制中第二低位1的位权,即(i-2^{k1})的二进制中最低位1的位权。
即sum_7=c[(111)_2]+c[(110)_2]+c[(100)_2]=c[(111)_2]+c[(111)_2-2^0]+c[((111)_2-2^0)-2^1]
综上我们发现,树状数组是对二进制的灵活运用。
我们还发现,树状数组对最低位1有着灵活的应用,那么我们该怎么找这个最低位1以及他的位权呢?
其实,我们只需要得到最后一个1的位置,并且把除了这个位置以外的所有位置置成0即可。
所以我们有了第一种算法:2^k=x&(x^(x-1)):
我们用二进制下的0110即十进制下的6举个例子
(0110)_2-1=(0101)_2,在这一步中,我们达成了这个数的最后一个1开始到最后所有数都取反
(0110)_2^(0101)_2=(0011)_2,在这一步中,我们达成了最末位1之前的所有数都是0,后面(包括这个1)都是1
(0110)_2&(0011)_2=(0010)_2,在这一步中,我们达成了最末位1之前的所有数都是0,而最后一个1之后的所有数也都是0,只有这个1的位置是1,我们便得到答案了。
这个算法的灵性在于怎么灵活的运用位运算分别将之前和之后的所有位置置成0。
这样我们就找到了6的二进制中最低位1的位权即2.
另一种算法是:前人的智慧告诉我们,2^k=i&(-i),那么这个算法的原理何在呢?
2.3 lowbit
$2^k=$i&(-i)
2.3.1 原码,反码和补码
我们首先来看二进制的相关知识:原码,反码和补码
我们首先知道正数的原码,反码和补码都一样
然后来看负数,我们给出一个8位二进制负数(10101011)_2,
反码就是在原码的基础上,符号位不变,其余各位取反:原码[10101011]=反码[11010100]
补码就是在反码的基础上按照正常的加法运算+1:原码[10101011]=反码[11010100]=补码[11010101]
PS:反码和补码的引入是为了方便计算机计算的,感兴趣可以自己了解
2.3.2 lowbit
负数的存储特性是:负数是以补码存储的。
那么我们来看x&(-x):
还用二进制下的的0110即十进制下的6来举例子,那二进制下的1110即十进制下的-6,(这里是4位二进制)
我们刨除符号位来看剩余部分,因为负数按补码形式存储,我们来看原码[110]=补码[010]
然后(110)&(010)=(010),就找到最末位1了,很神奇。
原理在于:补码的性质是原码取反+1,我们关注最末位1和它的前后,原码取反后+1,使得最末位1变为1,后面所有数变为0,然后x&x的补码,就有最末位1之前的所有数都是0(与运算和取反运算结合),而最后一个1之后的所有数也都是0(补码的最末位1后面所有数都是0,然后与运算),只有这个1的位置是1(原码和补码的这一位都是1),最后符号位进行与运算后保证是正数。再举例(43)_{10}=(00101011)_2
2.4 树状数组的实现原理
树状数组的实现一般也是:单点修改,单点查询,区间修改,区间查询。
以下内容由上图即16个数据的树状数组举例。
2.4.1 单点修改
比如我们要修改a[5]的值,只需要修改c[5],c[6],c[8],c[16]。
怎么算呢+只需要递推修改x,每次加上lowbit(x)即可。
即a[i]包含于c[i+2^{k1}],c[(i+2^{k1})+2^{k2}]···
2.4.2 查询
大家看到小标题写的是查询而不是单点查询/区间查询,为什么呢?
这是因为,在树状数组中,我们是没有办法维护区间和的,所以想要求区间和怎么办呢?
我们维护前缀和,然后用y的前缀和-(x-1)的前缀和就是区间[x,y]的和了。
所以,我们在树状数组中一般维护的都是前缀性的东西。
所以这里我们来看例7:[模板]树状数组1:P3374传送门
题目大意:单点修改,区间查询
实例代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
#include <iostream> using namespace std; #define MAX_N 500010 int tree[500010] = { 0 }; int n, m, c, x, k; int lowbit(int x) { return x & (-x); } void add(int x, int k) { while (x <= MAX_N) { tree[x] += k; x += lowbit(x); } return; } int find(int x) { int ans = 0; while (x) { ans += tree[x]; x -= lowbit(x); } return ans; } int main() { cin >> n >> m; for (int i = 1; i <= n; i++) { cin >> k; add(i, k); } while (m--) { cin >> c >> x >> k; if (c == 1)add(x, k); else cout << find(k) - find(x - 1) << endl; } return 0; } |
2.4.3 区间修改
如果题目让你把[x,y]区间内的所有值全部加或减k,那么怎么操作呢?
对于树状数组,我们好像只能将x,x+1,…,y每一个值都单独修改一遍,但是这样做复杂度一定很难受。
所以我们要换一种思路,即不能用原有数据维护前缀和建树。
那么我们引入差分。
(1)什么是差分
如果有b[1]=a[1],b[j]=a[j]-a[j-1],则a[j]=b[j]+b[j-1]+…+b[1]。
即a[i]=\sum_{j=1}^{i}d[j]。
例如:
| 原始数组a | 9 | 3 | 6 | 2 | 6 | 8 |
|---|---|---|---|---|---|---|
| 差分数组b | 9 | -6 | 3 | -4 | 4 | 2 |
a[4]=b[4]+b[3]+b[2]+b[1]=2。
然后给定一个任务:把区间[l,r]所有数加上k。(假设是[2,4])
| 加k后数组a | 9 | 5 | 8 | 4 | 6 | 8 |
|---|---|---|---|---|---|---|
| 差分数组b | 9 | -4 | 3 | -4 | 2 | 2 |
我们发现,差分数组b中只有b[2]和b[5]的值改变了。
原理手推一下就很好理解。
所以利用差分数组解决区间修改的问题,就可以得出公式:b[l]+=k,b[j+1]-=k。
(2)利用差分进行区间修改
我们用树状数组维护前i项差值和,即tree[i]=\sum_{j=1}^id[j],其中d[j]=a[j]-a[i]。
区间修改时只需要修改t[l]和t[r+1]即可。
利用这个原理我们还可以在维护差分数组前缀和时进行区间查询。
(3)利用差分进行区间查询
由上面\sum_{i=1}^{n}a[i]=\sum_{i=1}^{n}\sum_{j=1}^{i}d[j],我们可以推导
a[1]+a[2]+…+a[n],
=(d[1])+(d[1]+d[2])+…+(d[1]+d[2]+…d[n]),
=n×d[1]+(n-1)×d[2]+…+d[n],
,=n×(d[1]+d[2]+…d[n])-(0×d[1]+1×d[2]+…+(n-1)×d[n]),
即\sum_{i=1}^{n}a[i]=n×\sum_{i=1}^{n}d[i]-\sum_{i=1}^{n}(d[i]×(i-1))。
所以我们维护tree1[i]=\sum_{i=1}^{n}d[i],tree2[i]=\sum_{i=1}^{n}(d[i]×(i-1))即可。
例8:[模板]树状数组2:P3368传送门
题目大意:区间修改,单点查询
实例代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <cstdio> using namespace std; #define MAX_N 500010 int n, m; int a[500010]; int tree[500010]; int lowbit(int x) { return x & (-x); } void build(int x, int k) { while (x <= MAX_N) { tree[x] += k; x += lowbit(x); } return; } int find(int x) { int ans = 0; while (x) { ans += tree[x]; x -= lowbit(x); } return ans; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { scanf("%d", &a[i]); build(i, a[i] - a[i - 1]); } int c, x, y, k; while (m--) { scanf("%d%d", &c, &x); if (c == 1) { scanf("%d%d", &y, &k); build(x, k); build(y + 1, -k); } else printf("%d\n",find(x)); } return 0; } |
