文章目录
展开0.写在前面
本篇介绍图论基础,最小生成树,最短路,割点割边,二分图匹配。
图论是算法中的大块,并且与工作实战会有紧密结合。
得图论者得天下。
0.0 什么是图
0.1 如何存图
1.最小生成树
2.最短路
3.割点,割边
3.0 概念定义
割点和割边都是无向连通图中的概念。
割点就是一个点,删了它及它连接的边,图就不再连通。
割边又被叫做桥,就是一条边,删了它,图就不再连通。
以下以求解割点为例。
3.1 暴力求解
我们可以暴力枚举点并删除,然后搜索整个图判断连通分量是否增加。如果增加,说明删掉的是割点。
真正求解时,我们可以只给枚举删除的点打上标记,搜到它的时候跳过即可。并不需要真正的删除。
如何求连通分量可以考虑使用并查集,以这道题为例: CF1242B 0-1 MST 。
暴力的做法拥有较高的时间复杂度,有兴趣可以实现,练练码力。
3.2 Tarjan算法
Tarjan ,图论大师,以 LCA 和 强连通分量 闻名。
这里的 Tarjan 算法主要利用了两个数组,分别为 dfn[\ ] 和 low[\ ] 。
我们借用 nullzx 的图来进行讲解。
我们都会 DFS 遍历一个图, Tarjan 的本质也是 DFS ,不过它只需一次。
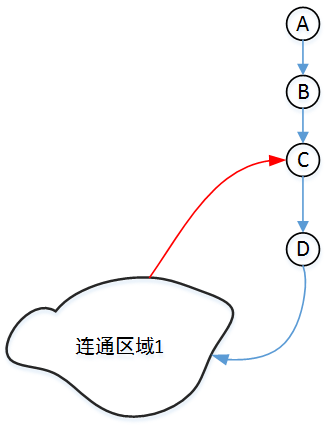
图中蓝色路径为 DFS 的边,我们称之为树边,所有蓝色的边与结点在一起组成的就是搜索树。
图中红色路径为 DFS 时碰到已搜索过点的边,我们称之为回边,表示我们通过这条边可以回到当前结点的祖先处。特别的,如上图, 连通区域1 内的所有点和 点D 都可以通过回边回到 点C 处。此情况我们称为 不经过父节点能返回祖先 。
dfn[\ ] 表示搜索的顺序,又称时间戳。
low[\ ] 表示 不经过父节点能返回祖先 最小的时间戳。
我们要在 DFS 时更新上述两个数组。
具体的模拟过程可以参考 nullzx 。
我们将其汇总成如下步骤:
- 取任意一结点作为树根。
- 赋当前节点的 dfn[u],low[u] ,遍历该节点 u 的所有出边。
- 如果得到的点 v 已经遍历过,则跳转步骤 4. ;否则,跳转步骤 2. 。
- 返回点 u ,更新节点的 low[u]=min{low[u],low[v]} 。
想判断某点 u 是否为割点,即将 dfn[u] 和它的所有孩子节点的 low 值做比较,如果存在至少一个孩子节点 v 满足 low[v]>=dnf[u] ,说明节点 v 必须通过节点 u 才能访问节点 u 的祖先,说明不存在节点 v 到节点 u 的祖先的其他路径,所以节点 u 是一个割点。
割点部分参考代码部分。
判断桥就更简单了,如果满足 low[v]>dnf[u] ,则说明边 u-v 是桥。
3.3 代码讲解
对于题目: P3388 【模板】割点(割顶) ,先贴出完整代码,并在代码中注释讲解:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
#include <iostream> #include <algorithm> using namespace std; #define N 20010 #define M 100010 int n,m,a,b,ans_cnt,d; int head[N],nxxt[2*M],to[2*M],cnt; int dfn[N],low[N]; int ans[N]; void add(int u,int v)//正常的前向星存图 { nxxt[++cnt]=head[u]; head[u]=cnt; to[cnt]=v; } void Tarjan(int u,int root)//Tarjan算法求割点 { dfn[u]=++d;low[u]=d;//遍历到的点首先赋dfn和low bool flag=false;//判断该点是否已经加入答案数组,防止重复加入。当然也可以开足够大的答案数组,在输出时特判 int cc=0;//根节点搜索树中的儿子个数 for(int i=head[u];i;i=nxxt[i])//遍历出边 { int v=to[i];//得到出点 if(!dfn[v])//如果出点没被遍历过,则进行遍历 { Tarjan(v,root); low[u]=min(low[u],low[v]);//回溯更新u的low值 if(low[v]>=dfn[u]&&!flag&&u!=root)//如果满足low[v]>=dfn[u],说明u是一个割点 { flag=true; ans[++ans_cnt]=u; } if(u==root)cc++;//根节点搜索树中儿子个数增一 } else low[u]=min(low[u],dfn[v]);//如果出点遍历过,则用出点的dfn更新当前点的low } if(u==root&&cc>=2)//如果是根节点且根节点搜索树中儿子个数大于等于二,说明根节点也是割点 ans[++ans_cnt]=u; } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) { scanf("%d%d",&a,&b); add(a,b);add(b,a);//无向边,建双向 } for(int i=1;i<=n;i++)//因为题目说图不一定联通,所以要判断每一个点是否枚举到。如果图联通,则直接Tarjan(1,1)即可 { if(!dfn[i]) Tarjan(i,i); } sort(ans+1,ans+1+ans_cnt);//对答案排序 printf("%d\n",ans_cnt); if(ans_cnt)//如果有答案,则输出答案数组(不加这句如果没有答案会多输出一个'0') { for(int i=1;i<ans_cnt;i++) printf("%d ",ans[i]); printf("%d\n",ans[ans_cnt]); } return 0; } |
下面强调两点:
- 对于根节点的特判。我们知道,对于根节点,如果
low[v]>=dfn[u],不能保证删除根节点图不再联通,如下图: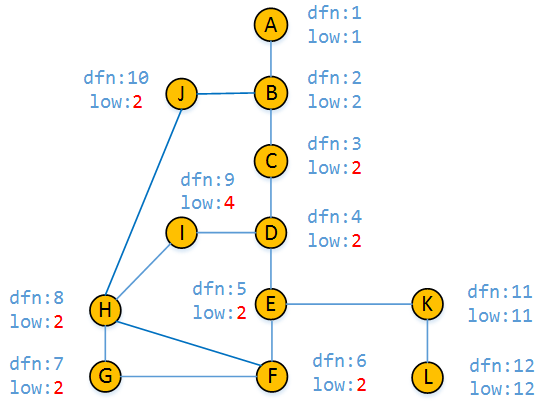
所以,对于根节点,我们要判断的是有几个搜索树中的儿子。原因是,如果根节点只有一个搜索树的儿子,说明删除根节点后搜索树仍是联通的,但如果根节点有两个搜索树的儿子,删除根节点后搜索树不再联通。比如说对于样例:

我们进行模拟后可以发现,它的搜索树是这个样子的:
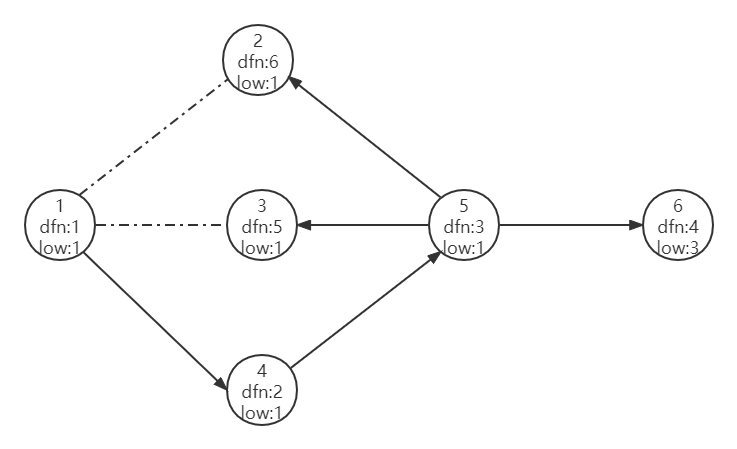
所以根节点 1 是只有一个搜索树里的儿子的。注意,此时点 2,3 并不是根节点 1 搜索树里的儿子。
所以,如果根节点在搜索树里只有一个儿子,说明删掉根节点图仍是连通的。但如果有两个儿子,删掉根节点后就不再联通了,这里不再举例子。
-
对于当遍历到已经遍历过点时,使用
low[u]=min(low[u],dfn[v])而不是low[u]=min(low[u],low[v])。原因是,当我们遍历到已遍历点时,这个已遍历点的 low 值可能已经改变,而我们经过回边能到达的仅仅是这个已遍历点,至于已遍历点的 low 值点,是不能仅仅通过这条回边到达的。用一下 _ztyqwq 的图:

我们可以发现,当我们遍历到点 3 时,它的 low 值被更新为 1 。但是当我们遍历到点 5 时,它的 low 值应该为 3 而不是 1 。同理,回溯到点 4 时,它的 low 也应该是 3 而不是 1 。如果 low[4]=1 的话,那么 3 就不再是割点。事实上它是,因为 4,5 都只能通过回边返回到 3 而不能再向上。
可以理解为此时 low 表示仅通过一条回边可以返回的 dfn 最小的祖先。这与 强连通分量 中的 low 值定义与运用有些不同, 强连通分量 中的我们在讲解到它时进行说明。
理解了上述强调的两点,代码别的部分基本就没有问题了。
4.二分图匹配
4.0 概念定义
4.0.1 二分图
一张图 G=<V,E> 是 二分图 ,当且仅当其点集 V 可以分为两个点集 V_0,V_1 ,满足 V_0\ \cup\ V_1=V 且 V_0\ \cap V_1 = \emptyset ,且对于图 G 的每条边 e_i ,其两个端点分别属于不同的点集。
其中, V_0 中的点称为 左部点 , V_1 中的点称为 右部点 。
4.0.2 匹配
图 G 的一个 匹配 是图 G 的一个边集 E_0 ,满足 E_0 的任意两条边都没有公共端点。
最大匹配 是指 匹配 中边数最多的一个。
4.1 匈牙利算法
二分图匹配的常见算法为匈牙利算法。过程如下:
首先枚举每一个左部点 u ,然后枚举 u 的出边得到出点 v 。对于出点 v ,如果没有匹配别的点,则直接进行 u,v 配对;否则,尝试让 v 的 “原配” 去匹配其他的点,如果 “原配” 匹配到了其他的点,则 u,v 配对;否则 u 失配。
模拟过程参考 一扶苏一 。
我们将其汇总成如下步骤:
- 遍历左部点得到 u 。
- 遍历 u 的所有出边得到出点 v 。
- 如果 v 没有匹配,则直接进行 u,v 配对,跳转步骤 1. ;否则,跳转步骤 4. 。
- 取 v 的 “原配” u’ ,跳转步骤 2. 。如果 u’ 匹配到了新的点,则 u,v 配对;否则, u 失配。
4.2 代码讲解
对于题目: P3386 【模板】二分图最大匹配 ,给出如下代码,并在注释中讲解:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
#include <iostream> #include <cstring> using namespace std; #define N 500 int n,m,e,a,b,ans; int edge[N+10][N+10]; int lans[N+10],rans[N+10]; bool flag[N+10],f; bool work(int x)//判断左部点x是否可以匹配别人 { for(int i=1;i<=edge[x][0];i++)//枚举左部点的所有出边 { int t=edge[x][i];//得到对应的右部点 if(!flag[t])//如果当前寻“原配”过程没有考虑过右部点t,则进行考虑 { if(!rans[t])//如果右部点没有匹配过,直接进行匹配 { lans[x]=t; rans[t]=x; return true; } flag[t]=true; if(work(rans[t]))//如果右部点的“原配”左部点可以匹配别人,则当前左右部点匹配 { lans[x]=t; rans[t]=x; return true; } } } return false;//如果整个过程结束后,仍不能匹配,说明左部点x不能匹配别人 } int main() { scanf("%d%d%d",&n,&m,&e); if(n>m)//如果左部点个数大于右部点个数,交换左右点集 { swap(n,m); f=1; } for(int i=1;i<=e;i++) { scanf("%d%d",&a,&b); if(f)edge[b][++edge[b][0]]=a;//存图方式要注意 else edge[a][++edge[a][0]]=b; } for(int i=1;i<=n;i++)//枚举左部点的每一个点 { for(int j=1;j<=edge[i][0];j++)//枚举每一个左部点的所有出边 { int t=edge[i][j];//得到对应的右部点 if(!rans[t])//如果右部点没有匹配过,直接进行匹配 { ans++; lans[i]=t; rans[t]=i; break; } memset(flag,false,sizeof(flag));//flag保证每次寻找“原配”时只判断一次 flag[t]=true; if(work(rans[t]))//如果右部点的“原配”左部点可以匹配别人,则当前左右部点匹配 { ans++; lans[i]=t; rans[t]=i; break; } } } printf("%d\n",ans); return 0; } |
针对上述代码,强调一下几点:
- 上述代码没有删重边,复杂度会相应提高,但可以过本题。可以尝试去除重边,这样复杂度会降低。
-
存图方式,如果单纯的用 O(n*m) 的邻接矩阵存,会爆时间,因为这样遍历的时候就变成了 O(n*m) 的复杂度,而用邻接表存遍历只需要 O(e) 的复杂度。当然,这里的遍历是指遍历所有边,要想使用匈牙利算法首先要遍历所有左部点,所以邻接矩阵的匈牙利算法时间复杂度约为 O(n^2*m) ,而邻接表的匈牙利算法时间复杂度仅为 O(n*e) 。上述中, n 表示左部点个数, m 表示右部点个数, e 表示边数。对于本题,大大降低了时间复杂度。
当然,上述代码还是使用了 O(n*m) 的表,如果想节约空间,可以使用
vector。特别的,如果想进一步优化的话。我们知道,将左右部点集交换对于结果没有影响,所以如果 n>m 的话,将左右部点集交换可以使得复杂度再减小一些。
这里的时间复杂度计算可能存在问题,希望大家指出。 一扶苏一 的时间复杂度证明为 O(n*e+m) ,暂未理解。
-
代码过程有些繁琐,但复杂度是正确的(可能会因为
memset增加一点常数)。 -
上图中,
flag数组保证了每次进行主函数中 “原配”匹配其他点 过程时,每个右部点仅被考虑一次。这样也降低了部分复杂度,如果一个右部点匹配过或不可以进行 修改原配 时,那么以后也不用考虑让它修改原配了。
综上,简单的匈牙利算法理解起来有些暴力,但是针对这个算法也可以提出如上的改进措施,使得复杂度大大降低,这就是算法优化的妙处所在。
最后,二分图匹配问题还可以使用 dinic算法 ,复杂度为 O(\sqrt{n}*e) 。但是此算法涉及网络流知识点,暂且不作掌握,若以后有机会再进行学习。
